ADVERTISEMENTS:
The following are some of the most important measures of studying variation in the data:
1. Range
2. Quartile deviation
ADVERTISEMENTS:
3. Mean deviation
4. Standard deviation
5. Coefficient of variation
6. Lorenz curve
Method # 1. Range:
ADVERTISEMENTS:
Range is the simplest measure of studying dispersion. It is the difference between the largest and smallest value in the distribution.
It is given by the formula-
Range = L – S Where, L = Largest value S = Smallest value
Calculation of Range:
ADVERTISEMENTS:
1. Individual Observations:
Individual observations refer to a group of individual items or individual values. In such a group, the range is calculated by deducting the lowest value from the highest value in the group or series.
2. Discrete Series:
Data is said to be discrete when the variable takes only particular values, that is, only integer values. For example, number of students in a class, results of rolling two dice etc., cannot have values as fractions.
ADVERTISEMENTS:
3. Continuous Series:
Continuous series can take any values in a given range. For example, the height of a person can be any value within the minimum and maximum height of human beings and when time is a variable, it can take any value and can also be measured to fractions of a second.
Range for a continuous series can be calculated by subtracting the midpoint of the lowest class from the midpoint of the highest class.
Merits of Range:
ADVERTISEMENTS:
1. Range is the simplest measure of dispersion among all the methods.
2. It is easy to understand.
3. It can be computed easily and quickly.
Demerits of Range:
1. It is not based on each and every variable in the data.
2. It fluctuates from sample to sample.
3. It cannot describe the characteristics of a distribution as it is merely based on two extreme values.
Method # 2. Quartile Deviation:
A quartile is a measure that divides the data into four quarters. The first quartile, denoted by Q1 lies in the middle of the first half of the data set. It covers the first 25 percent of the data set. The second quartile, denoted by Q2, divides the data such that 50 percent of the data lies below it and 50 percent of the data lies above it.
This is called as the median. The third quartile, denoted by Q3, lies in the middle of the second half of the data set. 75 percent of the data would lie below the third quartile and 25 percent of the data would be greater than the third quartile.
The interquartile range is a measure of absolute dispersion. It is calculated based on the lower quartile and the upper quartile, that is, the first quartile and the third quartile respectively. The interquartile range is the difference between the third quartile and the first quartile.
Interquartile range = Q3 – Q1
Quartile deviation is a measure that reduces the interquartile range to semi-quartile range. Quartile deviation is obtained by dividing the interquartile range by 2.
It gives the average value by which the two quartiles differ from the median value.
Computation of Quartile Deviations:
i. Individual Observations:
The important thing to be kept in mind while calculating first quartile and third quartile, in case of individual observations, is that the data set should first be arranged in an ascending or descending order. The formula for first quartile (Q1) is-
Where, N is the number of observations in the data set.
ii. Discrete Series:
In case of a discrete series, we first calculate the Cumulative Frequency (c.f.). Cumulative frequency is calculated by adding a class frequency and all class frequencies before it, in a frequency distribution.
The formulae for calculating Q1 and Q3 in this case, remain the same as the ones used in the case of individual observations.
iii. Continuous Series:
In case of continuous series, we first calculate cumulative frequency, as done in the case of discrete series.
However, the formulae used for calculating Q1and Q3 in this case are:
Merits of Quartile Deviation:
1. It is considered to be superior to range.
2. It is extremely useful in open end distributions (when one or more classes do not have a boundary) or when the data is ranked and measured quantitatively.
3. In case of skewed distributions, quartile deviation is an appropriate measure of dispersion as it is least affected by the presence of extreme values.
Demerits of Quartile Deviation:
1. It ignores 50 percent of the data as it considers only first 25 percent and last 25 percent of the data.
2. The value is not based on every item in the data.
3. It does not indicate how the values are dispersed around the average.
4. It does not facilitate further mathematical treatment.
Method # 3. Mean or Average Deviation:
The mean deviation, also known as the average deviation, is the average difference between the values in the distribution and the mean or the median. This method shows the average scatteredness of the values in the distribution around the mean or the median.
This means that the mean deviation can be calculated in the following two ways:
1. Mean Deviation (M.D.) about the mean value, and
2. Mean Deviation (M.D.) about the median value.
Computation of Mean Deviation:
1. Individual Observations:
In case of individual observations, mean deviation is calculated using the formula:
Where, n is the number of observations in a distribution.
X is a particular observation in the distribution, and
A is either the median value or the mean value.
| X – A | or | D | means that the deviation values are taken as absolute values.
2. Discrete Series:
In case of a discrete series, we first calculate the cumulative frequency (c.f.). Cumulative frequency is calculated by adding a class frequency and all class frequencies before it, in a frequency distribution.
The formula used for calculating mean deviation in this case is:
Where, N is the total of all frequencies in a distribution, is the frequency of any given observation, X is a particular observation in the distribution, and A is either the median value or the mean value.
| X – A | or | D | means that the deviation values are taken as absolute values.
3. Continuous Series:
In case of a continuous series, the formula used for calculating mean deviation remains the same as stated in the case of discrete series with one important exception that now, the deviations are the difference between midpoints of various classes and the mean or the median value.
Where, N is the total of all frequencies in a distribution, is the frequency of a class interval, m is the mid-point of the class intervals, and A is either the median or the mean value.
| m – A | or | D | means that the deviation values from mid-points of class intervals are taken as absolute values.
Merits of Mean Deviation:
1. It is simple to understand.
2. It is easy to compute.
3. It is based on each and every value in the data set.
4. It is less affected by the presence of extreme values.
5. It facilitates comparison of two or more data sets.
Demerits of Mean Deviation:
1. It ignores the algebraic signs, that is, the positive and the negative signs. This means that it takes only absolute deviations. Thus, it is not very accurate.
2. It does not support further algebraic treatment.
Method # 4. Standard Deviation:
Standard deviation is the square root of the average of the squared deviations from the mean. It measures the absolute deviation of the values from the mean. Greater the value of standard deviation, greater is the deviation of the values from the mean.
Computation of Standard Deviation:
1. Individual Observations:
(i) Direct Method:
In case of individual observations, the formula used for calculating standard deviation using direct method is-
(ii) Assumed Mean Method:
Standard deviation can also be calculated by assumed mean method using the following formula-
Where, d = X – A and it represents deviations from assumed mean.
A = assumed mean
X = any particular observation in the data.
N = number of observations in the data.
2. Discrete Series:
(i) Direct Method:
In case of a discrete series, standard deviation is calculated using the formula given below:
(ii) Assumed Mean Method:
Using the method of assumed mean, the standard deviation can be calculated for a discrete series using the following formula:
3. Continuous Series:
When the data is in the form of a continuous series then the midpoints of each class are taken as X and deviations of these mid points from assumed mean is calculated.
Step deviation method is the most commonly used method in case of a continuous data set. In a step deviation method, the mid-points are calculated and then the deviations of assumed mean from the mid-point is taken and divided by the width of the class interval.
The standard deviation is then calculated using the formula below:
Merits of Standard Deviation:
1. Standard deviation is based on all the values in the data set.
2. It is definite and rigidly defined.
3. It supports further algebraic treatment.
4. Squaring of deviations eliminates the problem of algebraic signs that arises in mean deviation.
Demerits of Standard Deviation:
1. It gives more weight to the extreme items.
2. Calculation of standard deviation is cumbersome as compared to other measures of dispersion.
Method # 5. Coefficient of Variation:
Coefficient of Variation (C.V.) is measured by the ratio of the standard deviation to the mean. While the standard deviation is an absolute measure, the coefficient of variation is a relative measure. It is useful in comparing the variability between two sets of data.
Computation of Coefficient of Variation:
Merits of Coefficient of Variation:
1. Coefficient of variation is independent of unit of measurement as it is expressed as a percentage.
2. It facilitates comparison of data sets with different units of measurement and significantly different means.
3. It helps in measuring risk, especially in stock market investments.
Demerits of Coefficient of Variation:
1. Coefficient of variation cannot be computed if the mean of a data set is zero.
2. It is misleading when there are positive and negative values in a data set.
3. It cannot be used to determine the confidence interval for mean as in case of standard deviation.
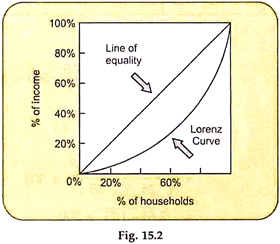
Method # 6. Lorenz Curve:
Lorenz curve is a graphical method of studying the dispersion of data, named after Dr. Max O. Lorenz, who developed it in 1905. He studied the dispersion of wealth by graphical method. In order to construct a Lorenz curve, the items as well as the frequencies are cumulated and the total is considered as 100 percentages.
Then percentages are calculated for the cumulated values. These percentages are plotted on a graph paper. If there is equal distribution of frequencies, the points would lie on a straight line. This line is known as the line of equal distribution or the line of equality.
However, if the distribution is unequal, the curve would be away from the line of equality. The farther the curve from the line of equal distribution, the higher is the inequality or dispersion. Given below is the Lorenz curve depicting income distribution among households.









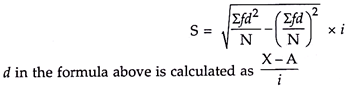
Comments are closed.