ADVERTISEMENTS:
In this article we will discuss about the methods and formulas used for measuring or calculating the price elasticity of demand with the help of suitable examples.
Answer 1. Measuring Price Elasticity of Demand:
Elasticity of demand can be measured by the following methods:
1. Proportionate or percentage method
ADVERTISEMENTS:
2. Point method
4. Total outlay or Total expenditure method
1. Proportionate or Percentage Method:
According to this method, price elasticity of demand (ep) is measured by using the formula explained under the concept of price elasticity of demand. It is —
This method is suitable to estimate price elasticity when the change in price is infinitely small. This can be understood from the following illustration.
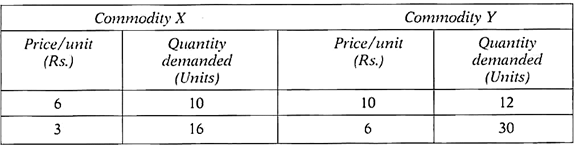
Example 1:
From the given demand schedules of goods A and B, find out which goods has a more elastic demand.
Comment:
Goods Y (3.75) has more elastic demand than the Goods X (1.2), the negative sign being ignored.
2. Point Elasticity Method or Geometric Method:
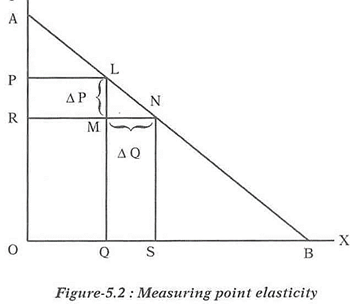
Point elasticity method is used to measure the elasticity of demand at a point on a demand curve when the change in price is very small. The price change is so small that the initial price and the changed price can be represented by the same point on price axis under the rule of approximation.
According to Leftwitch, elasticity computed at a single point on the (demand) curve for an infinitely small change in price is point elasticity.
ADVERTISEMENTS:
Point elasticity on a point of a linear demand curve depends on the slope of the curve and the price-output ratio at that point. Thus, elasticity of demand will be different at different points on the demand curve since the price-output ratio will be very. To show it geometrically, let us consider a point L on a linear demand curve AB, as shown in Figure-5.2.
For the sake of understanding, the two prices are shown by a good margin on price axis; though in reality the difference between the two is very small. Elasticity of demand can be measured as —
As per the Figure-5.2, price (P1) = OP = LQ and quantity (Q1) = OQ
ADVERTISEMENTS:
When price falls from OP to OR, the consumer moves from point L to point N on the demand curve. Then the —
Thus, the elasticity of demand is –
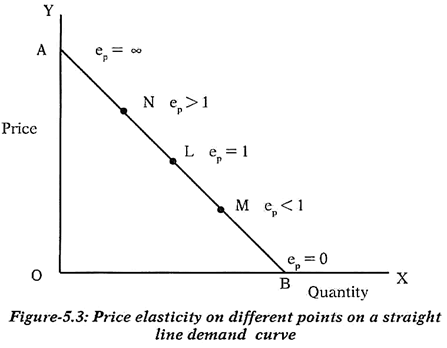
Given this, we can estimate price elasticity of demand at various points on the demand curve. This has been attempted in the Figure-5.3.
The figure shows that at point L, which is midpoint of the demand curve AB, LB = LA. Hence, the price elasticity of demand will be —
Thus, on a straight line demand curve, price elasticity will be different on different points. It can be understood by an alternative way as well.
In terms of proportionate method, it can be stated that the slope, and hence the reciprocal of the slope, will be same on all the points of the demand curve for being a straight line. Any difference in the price elasticity will be, therefore, due to the price-quantity ratio (P/Q) which will differ from point to point.
This can be shown as follows:
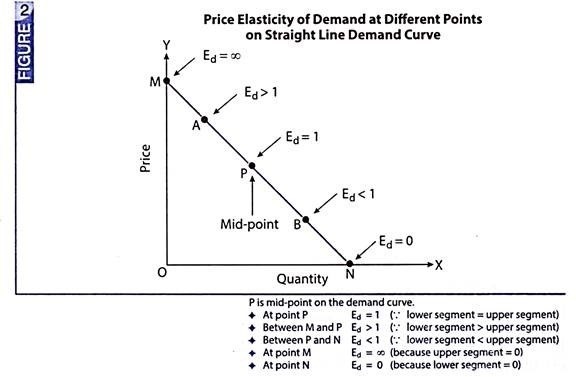
1. At a point located on the quantity axis, price will be zero and hence P/Q = 0 since zero divided by a positive number will produce a zero. This shows a perfectly inelastic demand.
2. Similarly, at a point located on the price axis, quantity will be zero and hence P/Q = ∞ since a positive number divided by zero will produce an undefined result. This shows a perfectly elastic demand.
3. In the same fashion, one can argue that at the mid-point of the demand curve, price will be equal to quantity and hence the P/Q = 1 resulting into a unit elasticity.
4. At a point located left of the mid-point, quantity will fall and price will rise. This will produce a greater than one value of the P/Q and, hence elastic demand.
5. Similarly, at a point located right of the mid-point, quantity will rise and price will fall. This will produce a less than one value of the P/Q and, hence an inelastic demand.
3. Arc Elasticity Method:
The proportionate method, suffers from a serious drawback which is that it gives significantly different estimates of the price elasticity of demand when we consider a fall in price or a rise in price within a same case. Such a problem does not occur in the point method since it applies only when the price change is very small and hence represented by just a point on the demand curve under the rule of approximation.
When the price change is large, point method cannot be applied and hence elasticity is to be estimated through the proportionate method which gives significantly different results. To overcome the problem, the elasticity is estimated with the help of the Arc elasticity method taking the two points forming an arc. This method measures elasticity by way of average responsiveness to price change shown over some definite portion on a demand curve.
Arc elasticity is the elasticity at the mid-point of an arc of a demand curve (Watson).
The arc elasticity method is based upon average price and average quantity in place of initial price and initial quantity respectively. In Figure-5.4, points A and B on the demand curve Dd represent new and initial points with the price levels as P2 and P1 and quantity levels as Q2 and Q1 respectively.
Taking the above Figure into consideration, the average price (P) and average quantity (Q) over the arc AB can be written as —
Thus, the arc elasticity measures the average elasticity, that is, at the midpoint of the chord AB. If the price of the goods increases or decreases in the same ratio and consequently demand also contracts and extends in the same manner then elasticity of demand will remain the same. But if proportionate method is used we will get different results.
Arc elasticity method is, thus, more realistic and dependable than the proportionate method. Hence, given the option, arc method should be preferred over the percentage method. It means that unless specifically asked to apply a particular method, we should use the arc method which is more trustworthy in terms of result.
4. Total Expenditure Method:
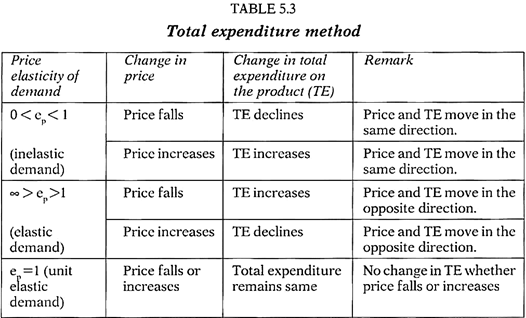
The total expenditure method was given by Marshall. Though, it is a very simple method, it does not provide an exact estimate of the elasticity, as the other methods do. It only shows whether elasticity is equal to one, more than one or less than one.
It evaluates elasticity on the basis of a change in consumer’s total expenditure (i.e. price multiplied by quantity) on the product as price of the product changes (See Table-5.3). It is also called as a total outlay or revenue method.
The table simply highlights the fact that if both the price of the product and the total expenditure on the product moves in the same direction, the price elasticity of demand will be less than one (ep < 1); if they move in opposite direction then the elasticity will be greater than one (ep > 1); and if there is no change in total expenditure with a fall or rise in price the elasticity will be equal to one (ep = 1). Following illustration further helps in understanding the method.
We are provided with data on price and quantity demanded of a product.
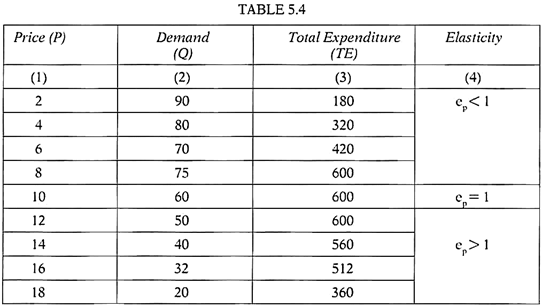
From it, we can show the elasticity of demand with the help of total expenditure method as given in the Table-5.4:
The column (1) of the Table-5.4 provides different price levels of a product and the column (2) the quantity demanded. Based on the information provided, we calculate total expenditure at all the price levels in column 3. The last column of the table throws light on the price elasticity on the basis of rules framed in Table-5.3. Based on the behaviour of total expenditure as the price changes, we identify the level of elasticity and draw the Figure-5.5.
On the basis of Table and the Figure, following observations can be summarized:
1. Up to price Rs.8, total expenditure of the consumer has increased with successive increase in its price. That is, a movement in the same direction and, hence, the elasticity of demand is shown as less than one in the column 4 of the Table. In the Figure-5.5, it is shown as a positively sloped upward looking curve, BD.
2. Following this, the total expenditure remains same at Rs.600 even though the price continued to rise up to Rs.12. This is a case of unit elasticity which is represented by a vertically straight line (DC) parallel to Y-axis or the price axis.
3. A further increase in price results in a fall in total expenditure representing the movement in opposite direction and, hence, the elasticity is shown as greater than one. In the Figure-5.5, this has been indicated by a backward sloping curve (CA).
Relationship between Revenue and Price Elasticity of Demand:
Revenue can be defined as the sale proceeds of a firm by selling a certain amount of units at a given price.
There are three basic concepts to represent the revenue:
1. Total Revenue (TR = P x Q),
2. Average Revenue (AR = PQ/Q), and
3. Marginal Revenue (MR = TRN – TRN-1)
Where, P is the price, Q is the quantity, TR is the total revenue, AR is the average revenue, TRN is the total revenue of the N units of output and TRN-1 is the total revenue of the one less than N units of the output. It is clear from the above that AR = P.
The MR can be shown mathematically as the first derivative of TR when it is differentiated with respect to output, i.e.
Relationships between AR, MR and Elasticity of Demand:
To indicate the relationship between AR, MR and the ep, we start with the total revenue function which is —
Thus, the equation (12) shows the relationship between MR, AR and the elasticity of demand.
It can be redrafted as –
Based on equation (12 or 13), a relationship between AR and MR can be established at different values of elasticity of demand. For example, if the ep = 1 (i.e. unit elastic) then —
It implies that in case of unit elasticity, MR = 0. Similarly, it can be argued that, when ep > 1, MR will be positive (or more than 0) and if the ep < 1, the MR will be negative (or less than 0).
Answer 2. Measurement of the Price Elasticity of Demand
Whenever, the elasticity of demand is referred to or mentioned as highly elastic or less elastic, it is considered as a vague expression. In order to explain this concept, there must be some method to measure the elasticity of demand of a commodity. The economists have proposed three different methods to measure the elasticity of demand.
(I) Total Expenditure (Outlay) Method:
This method was given by PROF. MARSHALL, in this method total amount of expenditure, before and after the price change is compared.
1. Unitary Elasticity of Demand:
When the total amount spent, before and after the price change, remains the same, the elasticity is termed as Unitary elastic. Under such circumstances, the rise in price is balanced by the reduction in demand and vice-versa.
2. More than Unity:
When the total expenditure increases in response to price- reduction and decreases with the increase in price the elasticity is said to be more than unitary elastic.
3. Less than Unity:
When the total expenditure decreases with reduction in price or when the total expenditure increases with an increase in price, the elasticity of demand is less than unitary elastic.
To illustrate the above concept, a chart is given below, showing various data pertaining to the changes in total expenditure in response to price changes. In each case, the elasticity of demand is also mentioned.
(II) Proportional (Percentage) Method:
In this method, the percentage change in quantity demanded is compared with percentage change in price. This method of determining the elasticity of demand was proposed by PROF. A. MARSHALL.
If the percentage change in quantity demanded (extension or contraction), is proportional to percentage change in price, the elasticity is said to be unity. If the percentage change in quantity demanded is more than the percentage change in price, the elasticity is more than unity and if the percentage change in quantity demanded is less than percentage change in price, the elasticity of demand is less than unity.
Mathematically, the elasticity of demand is represented as below:
(III) Geometrical Method:
Instead of carrying out numerical calculations, the Geometrical Method is used to determine the elasticity of demand at a particular point of demand curve.
Fig. 8.9 represents a Demand Curve of a commodity. In this method, it is assumed that the demand curve is a straight line (for the purpose of simplicity in explaining the concept).
DD1 is the demand curve and P1, P2 and P3 are the points representing corresponding price and demand positions.
The elasticity of demand for each point is obtained by determining the ratio between lengths of lower section and upper section of the curve. Mathematically-
In all the above cases, the elasticity of demand has been calculated (determined) assuming that the price of the commodity itself changes. But the demand (and the elasticity of demand) is influenced by other factors also besides changes in its own price. These include factors like change in the income level and change in the prices of other commodities.
Answer 3. Measurement of Price Elasticity of Demand:
There are two important methods of measuring price elasticity of demand:
(1) Percentage Change Method, also called Proportionate Method
(2) Geometric Method.
Following is a detailed description of these methods:
(1) Percentage Change Method/Proportionate Method:
This is the most popular method of measuring price elasticity of demand. Under this method, elasticity of demand is measured by the ratio of the proportionate (percentage) change in quantity demanded to the proportionate (percentage) change in price.
It is worked out as under:
Examples:
Solution:
Example 2:
Solution:
(2) Geometric Method:
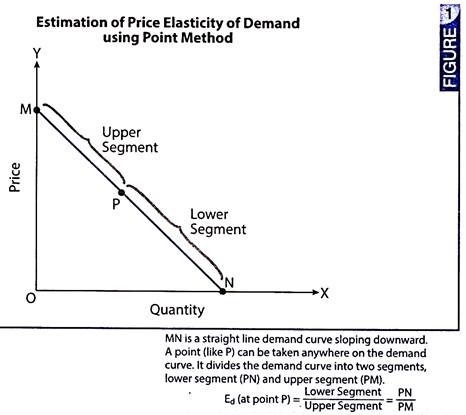
Geometric method measures price elasticity of demand at different points on the demand curve. It is also called ‘point method of measuring elasticity of demand’. As specified in the syllabus, we are to use this method only with reference to a linear demand curve, which is a straight line demand curve, as in Fig. 1.
In this figure, MN is a straight line demand curve. P is a specific point on the demand curve. The point P divides the demand curve into two segments, viz., lower segment PN and upper segment PM. Elasticity of demand at point P is estimated as the ratio between lower segment (PN) and upper segment (PM).
Fig. 2 illustrates this point further. It shows elasticity of demand at different points on a straight line demand curve.
Following situations are indicated in Fig. 2:


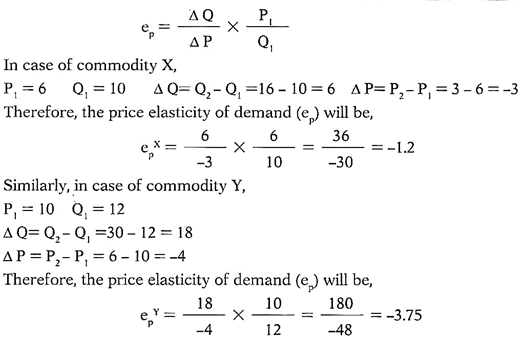
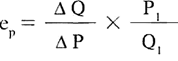
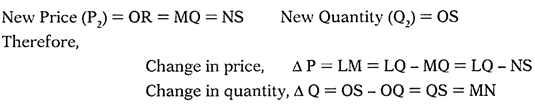





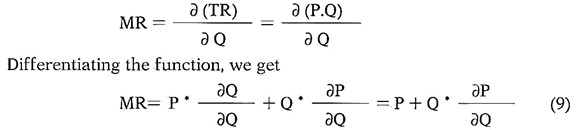

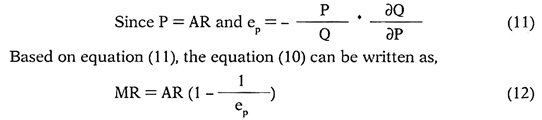


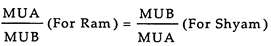




Comments are closed.